Understanding the Elo Rating System
In this article we’ll learn about the Elo Rating system. We’ll look at what problems it can be applied to and use visuals to help understand the math behind the equations.
Why you might need a rating system?
Before we go into the details about the algorithms behind the Elo Rating system let us take a step back and look at the problem we’re solving.
Imagine you are developing a game. In that game you have different players with different set of skills and experience who will compete against each other. Here are some goals for your game:
- If a lower skilled player (A) beats a higher skilled player (B), player A should be rewarded a lot because they were expected to lose, but won. Likewise, player B should be similarly penalized because they were expected to win, but lost!
- If a lower skilled player (A) loses to a higher skilled player (B), player A should not be penalized much because they were expected to lose and lost. Player B should not be rewarded much because they were expected to win and won.
- If equally skilled players compete neither is favored and should be equally rewarded or penalized.
- Discourage higher skilled players from competing against lower skilled players taking advantage of them.
- Over time as players skills change (hopefully increase) their associated rating should adapt.
It’s important to note that the changes in rewards is based on the difference between the expected outcome and the actual outcome. This will make sense later when we look at the equations.
I look around enough you will eventually come towards the Elo rating system as a way to solve these goals. If we change the words skill for rating and expected outcome for probability it can be easier to understand how these align. That system gives us a set of equations that allow computing players expected probability of winning and adjusting players ratings based on these outcome.
What is the Elo Rating System?
The system was developed by Arpad Elo originally to improve chess rating system, but as shown above can be used in any scenario where a rating system is needed. It is used in various professional sports leagues and E-sports games. Notably the Match Making Ranking (MMR) system of StarCraft 2
You may find more details from the wiki and we’ll walk through it below.
The system consists of two equations:
Given rating of player A and rating of player B compute the probability of player A winning and (vice versa)
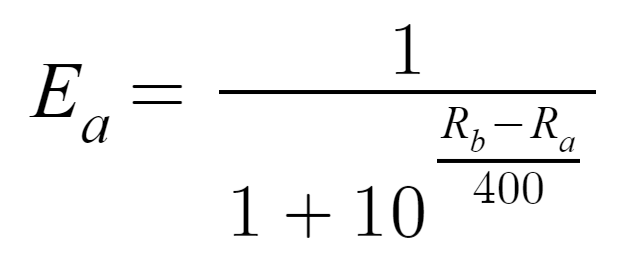
- The subscripts ‘a’ and ‘b’ to denote the player. Notice: this equation is for computing expected (E) probability for player A and the difference is Rb — Ra. There is a similar converse equation for player B with the subscripts reversed so that it contains Eb = 1/(1 + 10^(Ra - Rb)/400)
- The usage of the constant 400 can be adjusted based on how you want the expectations to correlate to the differences in ratings and we’ll look at this it in detail more later in the article.
2. Given the current player rating (R), the expected probability of winning (E) and the actual outcome (S)

- The K for K-factor and is another constant that can be be adjusted to control the sensitivity of the of the update. Too large and it will be to sensitive. Too little and it won’t be responsive.
- The S is from the word Score which is a fixed value in the range of the probability. 1 for a win, 0 for loss, and optionally 0.5 for draw if your game to supports this. I often refer to score as outcome in the article.
- If you remember the goals listed above you can see this is where the difference between the expected vs the actual effects the change.
If they were expected to lose but won, the difference will be almost ~1 and so they will gain almost all of K points. If they were expected to lose and lost, the difference will be almost ~0, thus K(~0) = ~0, and it will be negligible change.
How do these equations work?
It can be hard to visualize the outputs of these functions by only looking at the equations and theorizing about relationships between the numbers. We can use modern tools which allow us to visualize graphs and change parameters with a web interface to see these changes and get a better intuition.
Video 1: How logistic distributions are used to visualize potential player score and compute the probability of player score
Link to Desmos graphs to play with the values yourself:
Video 2: Explaining how the difference between ratings affects the probability.
Link to Desmos graphs to play with the values yourself:
Video 3: Understanding the rating update algorithm and K factors
Link to Desmos graphs to play with the values yourself:
Resources:
Here are links to resources I used to produce this article which you may find helpful if you want more details.
Overview Video:
Application in NFL team ratings
- FiveThirtyEight application to NFL rantings: https://fivethirtyeight.com/features/introducing-nfl-elo-ratings/
- Slides: R, Data Wrangling & Predicting NFL with Elo like Nate SIlver & 538
Wikipedia
- Elo Rating System: https://en.wikipedia.org/wiki/Elo_rating_system
- Logistic Function: https://en.wikipedia.org/wiki/Logistic_function
- Based on: https://en.wikipedia.org/wiki/Logistic_distribution
Conclusion:
Hope that helps you understand why rating systems are useful, the math behind the Elo algorithms and the graphs can help you visualize the probabilities and rating changes.
Let me know what you think in the comments below. I found being able to slide values on graphs and click the intersection points was helpful for my understanding.
